Joint HM coupling: pore pressure diffusion stuck

3DEC
1

Hi there everyone!

So, we are running some tests for possible fault reactivation under given imposed pore pressure.

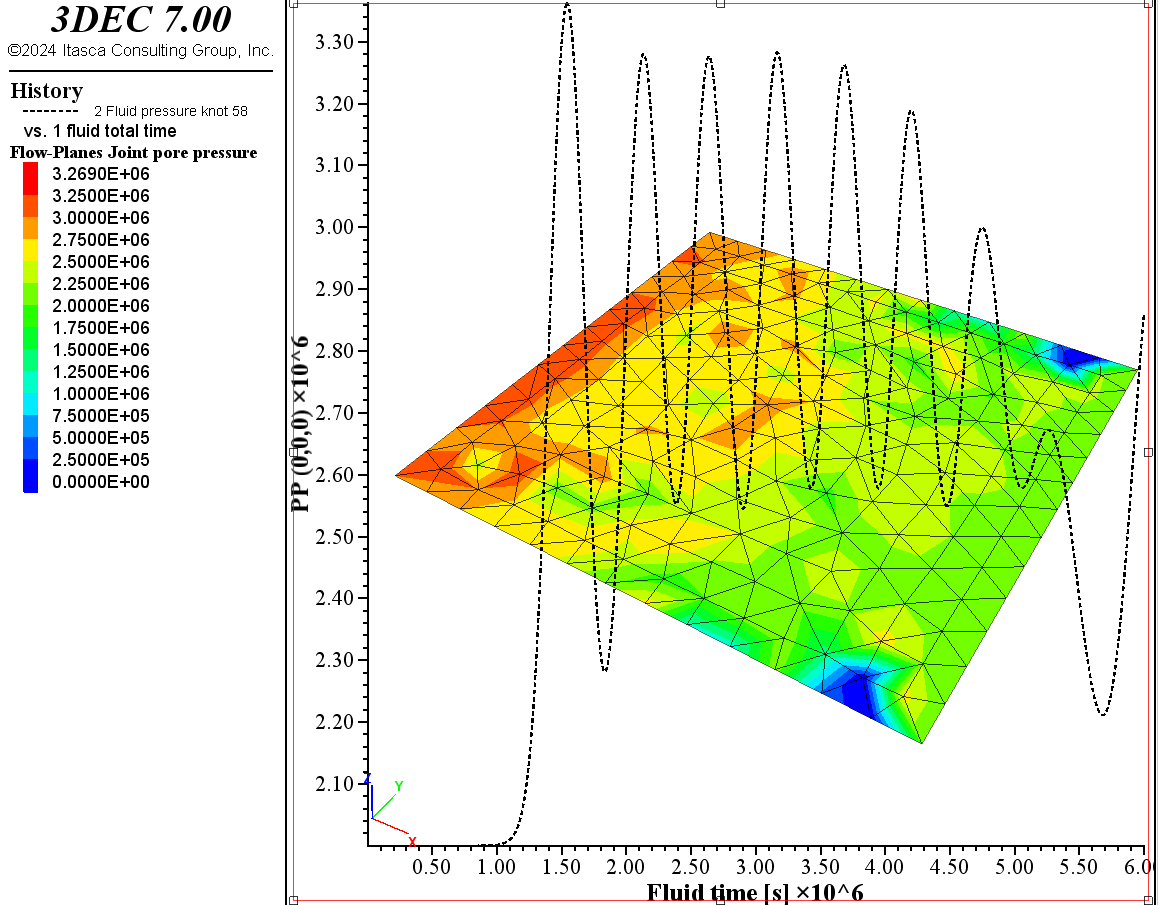
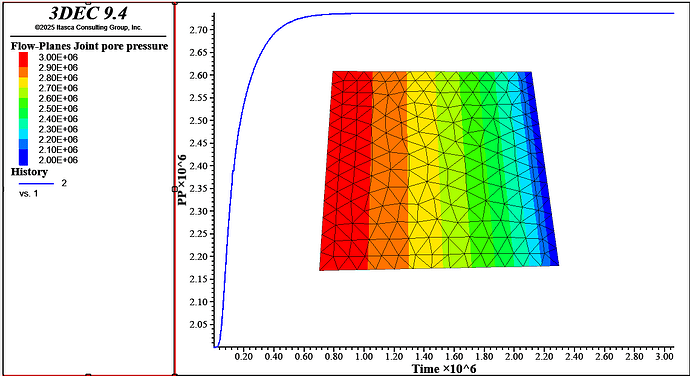
We started from the documentation example coupled-fast. When changing the model dimensions (from metric to kilometric scale), pressure does not propagate:

image
image1070×809 28.3 KB

We tried increasing the timestep and reducing the mesh size, but nothing changed.

Also, since we had to increase the mesh size, the apparent water bulk would greatly be reduced, hence getting out of the “incompressible fluid” necessity for fast-flow computations. We also ran the fully coupled script (without fast flow and with actual water bulk), but still no luck.

I provide the full script below.

Any advice welcome!

Cheers

Theophile

; fully coupled analysis with fast-flow
model new
model config fluid
model large-strain off

fish define set_props
    ;; Initial coupled-fast
    ;global xmin = -1.
    ;global xmax = 1.
    ;global ymin = xmin
    ;global ymax = xmax
    ;global zmin = xmin
    ;global zmax = xmax
    ;global z_jset = (zmin+zmax)/2.
    ;global edgelen = 0.25
    ;global ncycles = 2500
    
    ; Upscaled
    global xmin = -4000.
    global xmax = 4000.
    global ymin = -3000.
    global ymax = 3000.
    global zmin = -3000.
    global zmax = 0.
    global z_jset = (zmin+zmax)/2.
    global edgelen = 250.
    global ncycles = 10000

end
[set_props]

block create brick [xmin],[xmax] [ymin],[ymax] [zmin],[zmax]
block cut joint-set dip 0 dip-direction 90 origin 0 0 [z_jset]

block zone generate edgelength [edgelen]
block zone cmodel assign elastic
block zone prop density 2500 shear 2e9 bulk 5e9

block contact jmodel assign mohr
block contact property stiffness-normal 1e10 stiffness-shear 1e10 

flowplane vertex property aperture-initial 1e-4 ...
                          aperture-minimum 1e-5 aperture-maximum 1e-3

block fluid property bulk 2e9 density 1000 viscosity 1e-3

block gridpoint apply vel-x 0.0 range pos-x [xmin]
block gridpoint apply vel-x 0.0 range pos-x [xmax]
block gridpoint apply vel-y 0.0 range pos-y [ymin]
block gridpoint apply vel-y 0.0 range pos-y [ymax]
block gridpoint apply vel-z 0.0 range pos-z [zmin]
block gridpoint apply vel-z 0.0 range pos-z [zmax]

block insitu stress -1e7 -1e7 -1e7 0 0 0 nodis
block insitu p-p 2e6

; initial equilibrium - mechanical
model fluid active off
block fluid property bulk 0.0
model hist mech unbal-max
model cyc 100

; inital equilibrium - fluid
model fluid active on
model mech active off
block fluid property bulk 2e9
model cyc 100

block gridpoint ini disp 0 0 0
block contact reset disp 

flowknot apply p-p 3.0e6 range pos-x [xmin]
flowknot apply p-p 2.0e6 range pos-x [xmax]

block fluid fast-flow active on

model mech active on
block fluid property bulk [2e9/edgelen^3]
model mechanical substep 2000 
model mechanical slave on

history delete
model his fluid time-total
flowknot his p-p pos 0 0 [z_jset]

model fluid timestep max 1e-3
model solve fluid cycles [ncycles] or mechanical ratio 1e-6

;model save "coupled-fast"
2

The problem here is that your model is about 1000x bigger than the example, but the max fluid timestep is still set to 1e-3. If you change this to 1 (or 10, or 100) you will see some action. It will still take some time though - this mesh is quite a bit denser than the one in the example.